January 04, 2021
Solow Growth Model - Overview, Assumptions, and How to Solve
No 1 Assignment Help
is only a click away.
We have developed a team where only subject-matter and experienced writers are available to look into the assignments and complete the write-ups. However, such details will be discussed further but before that let’s have a quick view to Solow Growth Model.
Introduction to Solow Growth Model
The Solow Growth Model can be termed as an exogenous economic growth model which is used to analyse the change in the economic output over the time in the saving rate, population growth rate, and technological progress.
The Solow Growth Model was created by the economist Robert Merton Solow. He also won the Nobel Prize and was the first neo-classical growth model. This model was generally based on the Keynesian Harrod-Domar model. The Solow model can be said as the base for the economic growth of modern theory.
Basic Representation of the Solow Growth Model
We are here to help you with all your queries no matter whether it is related to assignment writing or gaining knowledge. However, our professionals providing economics assignment help in Australia have simplified the Solow Model Theory.
Assumptions:
Let’s suppose that the population growth is represented by g. Similarly, the current population is denoted by N and future population growth is denoted by N’. All these are linked with the population growth equation N’ = N (1+g). For example, if the existing population is 100 and the population growth rate is 2%, then the future population will be 102.
All customers or buyers save a constant proportion in the economy which is represented by ‘S’, of their consumption and income. Thus, consumption is written as C and output is denoted by Y. These both are linked with the consumption equation which states that C= (1+s) Y. For instance, if a customer earns 100 output units as his/her income and the savings rate is 40%, then he/she saves 40 units and consumes 60 units.
The firms engaged in the economy generally create output by making the use of the same production technology which is used in labour and capital as inputs. Hence, the output level is written as Y, the labour level is L and the capital level by K. All these terms are linked with the production function equation which states that Y = aF (K, L).
The Solow Growth Model developed by Robert Solow accepts that the production function shows constant-returns-to-scale which is also known as CRS. In this assumption, if the capital stock is labour level becomes double, then the output level will be exactly 2x. Consequently, many of the mathematical analysis of the Solow model concentrated on the capital per worker and output per worker instead of aggregate capital stock and aggregate output.
The existing capital stock which is generally written as K, K’ stands for future capital stock, the capital depreciation rate is denoted by d, and capital investment level is written as I which are related to the capital accumulation equation K’= K(1-d) + I.
How to solve the Solow Growth Model?
Wondering, how to solve the Solow Growth Model? Here are the methods discussed by our experts who have been providing economics assignment help in Australia since 2010.
Step 1: In this analysis, It is assumed that the production function has this form: Y = aKbL1-b where 0 < b < 1. It is also called the Cobb-Douglas production function. This function method is being used widely in the neoclassical production function.
Step 2: Hence, per worker output is illustrated under the given equation:
y = akb where y = Y/L (output per worker and k = K/L (capital stock per worker)
Step 3: In the competitive equilibrium assumption, we have:
- The expenditure and income identity that embraces as an equilibrium condition: Y = C + I
- Consumer’s budget constraint: Y = S + C
- Hence, in equilibrium, we get the following: I = S = sY
- The capital accumulation equation will be: K’ = (1–d)K + sY
Step 4: The below given equation defines the capital accumulation equation in per worker times: (1 + g) k’ = (1 – d) k + sy = (1 – d) k + saf (k) = (1 – d) k + sakb
Step 5: Steady-state has been used as the solution concept. According to our assignment help experts, the steady-state is said as a state in which the capital level per worker remains unchanged. A graph is given below:
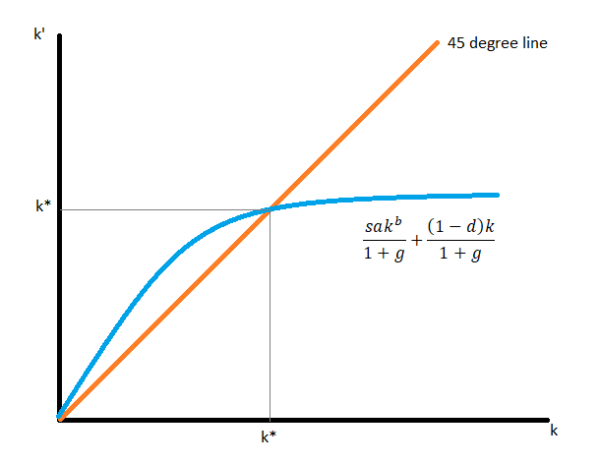
Step 6: Steady state can be identified by solving this equation: k’ = k => (1 + g)k = (1 – d)k + sakb
Step 7: Hence, the steady-state capital value per worker and the steady-state output value per worker will be like:
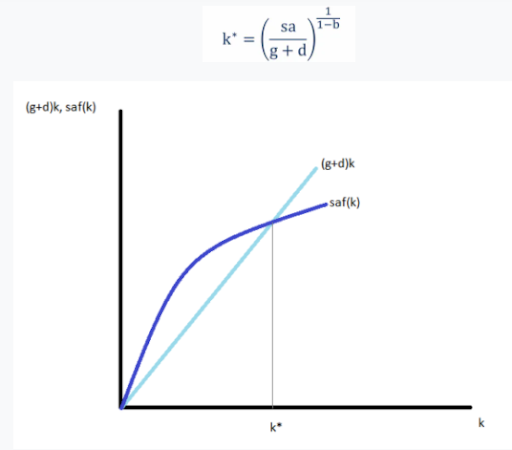
So, these were the steps that can be followed whenever you are asked to solve the Solow Growth Model. In case, if you are still encountering problems in your assignment then choose Online Assignment Expert. Contacting us to ensure you for the following:
- Downloading free samples
- Choosing own experts
- Getting unlimited revisions for free
- Help in different assignments such as essay, case study, research paper, dissertation, etc.
- Help in online quizzes and exams
- Proofreading and editing help
- Unique and original content
- Reasonable prices and more
Beyond this, there are many things you would like to know as we are the oldest and most availed assignment help service provider among students studying in Australian universities. We have provided best economics assignment help to scholars of Bond University, Deakin University, Australian Catholic University, Australian National University, CQ University, Charles Sturt University, Flinders University, and many more.
So, if you are a student enrolled at an Australian university and need assignment help, then let us know your requirement. We ensure that the best assignment help will be offered at a pocket-friendly price.
Related Blogs
Subscribe Our Newsletter & get Information about latest courses